Heron’s Fountain
The Alhambra, built by Nasrid Sultan Ibn al-Ahmar of Granada beginning AD1238, used a hydram to raise water. Through a first reservoir, filled by a channel from the Darro River, water emptied via a large vertical channel into a second reservoir beneath, creating a whirlpool that in turn propelled water through a much smaller pipe up six metres whilst most water drained into a second, slightly larger pipe.[1]
Leonardo Electronic Journal of Practices and Technologies
ISSN 1583-1078
Issue 11, July-December 2007
p. 59-70
Calvert (1957) evaluated the performance characteristics of hydraulic ram. The
possible independent variables of hydraulic ram installations were considered and with certain
assumptions their number reduced using dimensionless parameters such as the Reynolds
number, the Froude number, the Mach number, the head ratio and the coefficient of fluid
friction. The Reynolds numbers was known to be in effective in machines of practical size
and that a range exists over which the Mach number has little influence. The Froude number
was found to be the criteria for defining the possibility of operation of the ram and the ram
output and efficiency are dependent upon the head ratio.
In 1951, Krol [1] established that it was possible to forecast the behaviour of any
automatic hydraulic ram, provided the following properties at a given installation have been
determined separately.
• Loss of head due to impulse valve
• Drag coefficient of the impulse valve
• Loss of head in the pipe
• Head lost during the period of retardation.
According to Calvert (1960) the dimension of the drive pipe has a limiting value. This,
he established by applying dimensional analysis technique. The relevant parameters were the
head ratio, friction coefficient and the dimensionless numbers corresponding to those of
Froude, Reynolds and Mach. Hydraulic Ram for village use was developed by V.I.T.A in
USA [2]. The Ram was only used for small water supply with the impulse valve being
designed to act on a spring mechanism, while the delivery valve is a simple clack valve. A
general description of the hydraulic ram which solved most of the design problems was
undertaken by Molyneux [3].
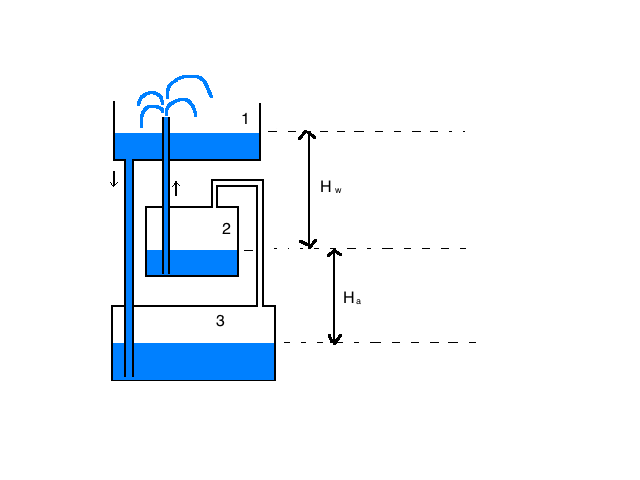
Description:
Heron’s fountain is a hydraulic machine that demonstrates the principles of hydraulics and pneumatics. Flow of water from high gravitational potential energy to low gravitational potential energy causes a fountain to form, due to increasing pressure on the inside of the system.
Materials:
- Two large jars with lids and basin
- 3 tubes to connect jars and basin together
- clamp
- Large volume of water and coffee containers to pour
- Towels
Demo:
The stepladder is a good frame for the Heron’s fountain demo as it allows you to change the relative heights of the containers to change the fountain effect. To start the demo container 1 must be empty, container 3 should have water up to the bottom of the straw, and container 2 should be completely filled with water.
There are three tube which be connected to the small glass straws sticking out of the lids of the jars. One tube must be going from the bottom of container 1 to the bottom of container 3, one from the top of container 3 to the top of container 2, and one from the bottom of container 2 through the floor of container 1 to form the fountain.
The tube leading from container 1 to container 3 should be primed before the demo is started. To do this you want to fill the tube with water (using a vacuum, siphon, etc.) and use the clamp to hold it closed while you connect it to the glass straw stemming from container 1. If this tube is not primed prior to use, the fountain will not work well. Priming the tube creates a large column of water quickly that would otherwise take time to form. The height of this column of water is what drives the fountain, as is discussed more in depth later.
Notes:
- A bigger effect will be seen when the distance between 1 and 3 vertically is the greatest. The length of the tube is not important for the pressure calculations, only the vertical height is important. Because of this, in order to change the size of the fountain you need to raise or lower the containers: Simply putting in a longer tube will not change the height of the fountain.
Explanation:
As it is labelled in the preceding image, assume the top basin is
container 1, the middle basin is container 2 and the bottom basin is
container 3. The system has an effective height of 
To start the fountain, container 1 should be open to the air and holding no water. Container 2 should be filled to the top with water, container 3 should be filled with water to the bottom of the straw, and the tube from container 1 to 3 must be primed. To begin the fountain, pour water into container 1 until it is filled. Almost immediately you should see water spring up out of one of the holes in the top container.
Container 3 needs to have water filled up to the bottom of the straw because otherwise air can get into the straw and flow backwards into container 1, which impedes the flow of the water. Additionally, when bubbles of air exit this way, the pressure of the system is being released in the wrong direction. In order to drive the fountain we need high air pressure in container 3 which pushes the water down in container 2. If the air, instead of flowing into container 2 flows back up into container 1, the fountain will run slowly.
As water is poured into container 1, gravity pulls it down into container 3. The air filling container 3 is displaced by the denser water flowing down from the top, and rises up through the tube connecting container 3 to container 2. This air increases the pressure in container 2, which displaces the water that was previously occupying space. Because the pressure in container 2 is greater than atmospheric pressure, water will flow up the tube and form a fountain. The flow of water will stop once container 2 is empty of water.
This is not a perpetual motion device, although it may look like one. Eventually, all of the water in container 1 will drain to container 3, and there will be no longer be the pressure that was exerted on the system, driven by gravitational potential energy acting on container 1. While container 3 completely fills with water, container 2 loses all its water through the fountain and will fill with air. Once the level of the water in container 2 is below the level of the tube that connects container 2 to container 1, the fountain will stop. If you continue to pour water into the first container, the water level will rise up through container 3 and 2, following Pascal’s theory of communicating vessels. Communicating vessels are discussed more in depth here, on the page for our equilibrium tubes demonstration.
To increase the height of the fountain, you want to minimize 
To see why increasing 
Because the pressure is related to the height of a column of fluid, the tube leading from container 1 to container 3 needs to be completely filled with water for the fountain to run well. If there is a slow trickle of water out of the top container into container 3, even though there may be a large vertical distance, the fountain will not work well because there is not a continuous column of water that adds to the pressure of the system.
In addition to changing the heights of the columns, you can change the height of the fountain and the running time by changing the diameter of the tubes used for the fountain on the right side. A smaller diameter tube will mean a higher fountain and a longer run time; a larger diameter tube will lead to a shorter fountain and shorter run time. The containers are air tight, so there must be equal flow of water into the system as out of the system. If you put a small opening for the fountain, the water flow out of that will dictate the flow rate of the whole system, and there will be a large buildup of pressure in container 2 because water does not escape quickly. As the diameter of the fountain gets smaller, the pressure in container 2 will increase, which will push the water out at a higher velocity, increasing fountain height.
This demonstration can also be thought of as a siphon with the upper arch of the tube missing. In this example, the positive pressure of the bottom two containers is what drives the water to move. In a “typical” siphon, it is generally agreed that the force that pulls the water up through it is a negative pressure at the top of the bend. There is a more in-depth explanations of how siphons work here at the page discussing the Pythagorean Cup demonstration.
Possible variations or changes:
Change out tubes leading from container 3 to container 2 and container 2 to container 1 to show how the run time and fountain height changes with tube diameter (fountain should stay the same, run time should go down with increasing diameter.
Partially blocking or not priming the tube from container 1 to 3 so that only a small trickle of water can come out. Have the class explain why the fountain works best when the flow of water isn’t impeded in any way and when there is a tall column of water.
Written by: Sophia Sholtz
4.9 HYDRO POWER
4.9.1 Background and State-of-the-Art
i. The use of water power for irrigation
The main shortcoming of water power as an energy resource for irrigation is that it is only available for convenient use in a limited number of locations having suitable flows and heads to engineer an effective site. Also, most regions with hydro-potential tend also to have plentiful rainfall, which often makes irrigation a low priority as a hydro-power application. However, despite these drawbacks, there are many areas where rainfall is seasonal (eg. where water can usefully be applied during the hot dry summer months to gain an extra crop or to increase yields and, similarly, in mountainous areas, where snow-melt water often provides some limited hydro-potential in the dry summer season). However, steep hydraulic gradients in hilly country generally allow any valley floor areas to be gravity irrigated by digging contoured canals, which take water from a stream and direct it along the side of a valley at a lesser hydraulic gradient then the main stream. This practice is of course widespread in much of the central Asian massif. When gravity does the work, pumping techniques are generally not needed.
Therefore, the main applications for the use of water power to pump water will be in lowland areas, inevitably using low head water drops as a power source, to irrigate land which would not be accessible to gravity water flow. An obvious important application, common in China, is to extend the command area available to a gravity irrigation scheme to take in higher land above a dam. In some arid regions, or regions with dry seasons, there are large perennial rivers where the river current can be utilized to lift water which would otherwise flow past parched fields. Even in some wetter and more mountainous areas there are situations where water power could allow irrigation of terraces or plateaux that are inaccessible to gravity flow; this can be of importance where flat land with soil suitable for cultivation is scarce.
Given a suitable site in proximity to a suitable need, hydro-power has a number of important and fundamental attractions:
- it is generally available 24h/day
- it is a relatively concentrated energy source
- the available energy is easily predictable in areas where river flow data are available
It follows from these points that hydro-powered systems tend to have a high power to size ratio and hence a favourable power to cost ratio, they also tend to be mechanically simple and robust, and therefore have long working lives and require limited and simple maintenance. As a result hydro-power can be one of the most economic sources of power for those fortunate enough to have a suitable resource available.
ii. General principles
All water power applications involve removing energy from falling or flowing water. The power P available from a flow of Q litre/sec falling through a head of H m is:
Where 9.8 is the gravitational constant (in metric units of m/s2), and if Q is in m3/s, then the above formula gives P in kW. In otherwords there is 9.8kW available for a flow of lm3/s per meter drop. The actual output will be reduced by multiplying by the system efficiency; eg. a device with an efficiency of 50% will convert half the available power.
The efficiency of hydro-powered systems is high. A good small turbine will typically be 70% efficient and even water wheels and other more primitive devices tend to be 30 to 60% efficient, as indicated in Table 21.
Table 21 EFFICIENCY OF HYDRO POWERED SYSTEMS
|
type of device |
efficiency factor |
| (typical) | |
|
Undershot water wheel |
0.30-0.40 |
|
Vertical shaft water mill |
0.20-0.35 |
|
Poncelet undershot or Breast wheel |
0.50-0.65 |
|
Overshot water wheel |
0.50-0.70 |
|
Impulse turbine (eg Pelton) |
0.70-0.85 |
|
Reaction turbine (eg Francis, Prop.) |
0.60-0.80 |
|
Water pressure engine |
0.60-0.80 |
|
Turbine-pump |
0.35-0.50 |
|
Hydraulic ram (hydraulic output) |
0.30-0.60 |
|
River current converter |
0.25-0.30 |
Note that in all cases above, except turbine-pumps and hydraulic ram pumps, we are considering the conversion simply of water power to shaft power; to pump water then requires the addition of a pump or water lifting device which in turn will have further inherent inefficiencies. The exception has an efficiency figure relating to the hydraulic output divided by the hydraulic input, since there is no measurable intermediate production of shaft power.
It can be seen that the two key parameters required to estimate the power potential of a water resource are head and flow. Techniques for doing this are discussed in most references on micro-hydro power, such as [61] and [62], The static head is the most straightforward to measure; methods which can be used include:
|
- |
surveyor's levelling equipment; |
|
- |
spirit level, wooden pegs and straight edge; |
- |
a length of hosepipe with a pressure gauge (lm of water = O.lkg/cm2 or .098bar or or 1.42p.s.i. or 9.81kPa); the hosepipe is completely filled with water with its open end submerged in the upper water source and the other end fitted with the pressure gauge is held at the lower level to measure the actual static head; |
|
- |
barometer/altimeter (for higher head applications); (i.e. surveying barometer/altimeter) |
|
- |
accurate existing large-scale maps to take advantage of a previous survey |
The flow rate can vary a lot from season to season; obviously the key period of interest to farmers will be the irrigation season. With larger rivers, especially those having existing hydro-electric schemes on them, discharge measurements will already have been carried out and been recorded and will usually be available from the relevant river authority. However, in most cases involving small-scale equipment for hydro-powered water lifting it will only be of interest to consider quite small streams, rivers or canals, for which no data will be available. There is a variety of methods of stream gauging varying in sophistication and accuracy, such as:
- dam the stream and measure the overflow by measuring the time to fill a container;
- construct a small rectangular weir from wood or concrete and use the method given in Fig.140
- in streams where it is not practicable to build a
weir, measure
the depth of the stream at equal
intervals across its width (at a point where
the stream is straight and uniform) as in Fig. 141.
Then time a float drifting down the centre of
the measured section. This gives the
speed of the current at the centre of
the stream; the mean velocity will be 0.6-0.85 of this figure. A rough, rocky
stream bed requires a factor of 0.6, while smooth muddy surfaces require a
factor of 0.85. The flow is calculated from the product of the mean velocity
and area of stream cross-section using appropriate units:
e.g. velocity in m/s. x cross-section in m2 gives flow rate m3.
Obviously a current meter or a ship's log, if available, can more conveniently be used to measure the current velocity instead of timing a float. - dilution salt gauging is a new technique in which a known quantity of salt is poured into the centre of the stream at one point. An electrical conductivity meter is then used downstream from that point to measure the dilution. The data can then be used to determine the flow rate;
- use of automatic stream gauging instruments; a calibrated weir is used to derive the day by day river flow on an electric or clockwork water level recorder.
Fig. 140 Flow measurement with rectangular weir (after BYS Nepal)
Fig. 141 Method of stream gauging without the need to build a weir
In some cases it may be of interest to use river or canal current powered devices, in which case it is necessary to measure the current velocity either by timing the passage of a float thrown into the current between two points on land which can be aligned with it as it floats past, or a calibrated current metering device (or ship's log) can be used.
It is extremely difficult to estimate flow or current velocity by eye; human judgement is peculiarly bad at assessing these kinds of factors and very inaccurate results are likely.
4.9.2 Use of Turbines for Water Lifting
i. General types of turbine
As with pumps, there are families of different types of turbine to deal with different types of situation. Briefly, these can be characterized as follows:
| a. | low head | - | propeller/Kaplan |
| b. | medium head | - | Banki/Francis |
| c. | high head | - | Pelton/Turgo |
A typical small fixed blade propeller turbine is shown in Fig. 142 A. These are only adequately efficient over a narrow range of flows. Where variable flow and power is needed, adjustable gates are provided and the turbine runner may have fixed or adjustable pitch blades. The latter is known as a Kaplan turbine and is more efficient over a wider range of flows than a fixed pitch propeller turbine. But the complication of adjustable pitch runner blades is expensive, and therefore is only normally applied for larger-scale installations.
There is a middle head range of turbines, some of which involve mixed flow, rather like a mixed flow pump in reverse. Turbines of this kind run full of water, and are known generically as Reaction Turbines. The most widely used medium-head reaction turbine resembles a centrifugal pump (except the flow travels radially inwards from a spiral casing) and is a Francis turbine; Fig. 142 B. Reversed centrifugal pumps have actually been used as a cheap form of turbine, and can be quite acceptably efficient over a narrow range of flows and speeds at a given head. Another type of medium head turbine is known as the Banki (alias Ossberger, Mitchell or Cross-Flow) turbine. Here a jet of water impinges on a set of curved blades mounted between two discs, travels through the centre of the rotor and emerges from the far side again. Turbines of this kind do not run full of water and are known as impulse turbines in that they derive their rotation from deflecting a jet of water. High head applications are generally dealt with by another type of impulse turbine known as a Pelton Wheel (Fig. 142 C). With this a high speed jet of water is directed at a series of buckets set around the rim of the wheel. Each bucket has a central splitter which splits the jet in two and directs it almost back in the direction it came from and outwards from the rim of the wheel.
Fig. 142 Some of the main types of hydro turbine for low, medium and high heads
The reasons for using different turbine types at different heads and flows relate to the efficiency and speed of rotation that is required. Low head types of turbine, like propeller turbines have a high specific speed; this means they tend to rotate faster in relation to the velocity of the water travelling through them, which is important at low heads if electrical machinery, or rotodynamic pumps, are to be driven. However high heads would cause equipment of this kind to run at unacceptably high speeds, (and other problems would also occur) so lower specific speed types of turbine become necessary as the head increases. The interested reader should consult a standard text book on hydro-turbines as further discussion is beyond the scope of this work.
The shaft of a turbine can be connected directly to a generator, which then can be used to power electric pumps for irrigation, or it can be directly coupled to an appropriate centrifugal or other rotodynamic pump. The route via electricity is of interest in that irrigation water pumping is. highly seasonal, and a system which produces electricity can in many cases perform useful duties other than irrigation, such as providing light at night, post harvest processes, etc. However electricity generation inevitably involves a higher level of engineering sophistication and investment than is inherent in powering a simple pump by a simple turbine. Also, any hydro-electric plant needs to be well protected from flooding, while a simple turbine powering a pump is much less liable to damage and can therefore be more simply installed. There are also losses of efficiency inherent in converting shaft power to electricity, transmitting the electricity and then converting it back to shaft power; this could absorbe 25 to 40% of the energy converted.
The chosen approach must depend on the size of the hydraulic resource, and the potential for satisfying other economic applications, plus of course the financial and organizational resources of the user community.
ii. Chinese turbine-pumps
The Chinese have taken the combination of turbines and pumps to the logical conclusion of producing a large range of integrated turbine-pump units. Although this is a relatively recent development (originating in the early 1960s) some 60 000 turbine pumps were reportedly in use [63] irrigating 400 000ha by 1979.
Chinese turbine-pumps are generally for low head applications, where the hydro-power source will often be a canal jump in an irrigation scheme or a weir on a canalized river giving a head in the region of 1 to 15m. Therefore the turbine most commonly used is a fixed pitch propeller turbine which is appropriate for low heads. This is generally mounted with a vertical shaft surrounded by fixed gates; it therefore tends to be at its most efficient only over a narrow range of flow rates. A centrifugal pump impeller is mounted on the same shaft as the turbine, back-to-back as in Fig. 143. Where a high head water supply is needed, multi-stage centrifugal pumps may be connected to the turbine as in Fig. 144. In some cases an extension drive shaft can be fitted, as in Fig. 145; this allows the turbine to be used as a general power source at times when there is no demand for irrigation water. For example it can readily be applied to powering a small rice mill, oil expeller, generator, etc. This clearly can greatly enhance the economic value to be gained from the installation.
A large variety of different sizes and models of turbine pumps are made by numerous small manufacturers in China, and attractively low prices have been quoted for the export market. Table 22 indicates the range of sizes of single stage turbine pumps manufactured by a typical production unit, the Youxi Turbine-Pump Plant, Fujian, and the (1981) export prices quoted for these by the Fujian Provincial Agricultural Machinery Import & Export Corporation.
Because it can be misleading to make judgements on the economics of Chinese equipment on the basis of Chinese export prices converted at the prevailing exchange rate, some limited Chinese data on the relative costs of alternative pumping systems within the Chinese economy are of interest. It can be seen from Table 23 that turbine pumps are significantly cheaper than either electrically energized pumps or engine pumps, as is to be expected. Whether the same differentials would apply elsewhere is open to question, but the turbine-pump is almost certain to be economically attractive wherever there is the need for irrigation water combined with suitable installation sites.
Table 24 indicates the performance of a selection of small low, medium and high head turbine-pumps, including estimates of shaft power and efficiency. The overall efficiency is in the range 32 to 50% for the models considered; this implies that the turbines and pumps considered individually rather than in combination have efficiencies in the 56 to 71% range, assuming roughly equal efficiency for each. Other models exist with claimed overall efficiencies as high as 58%.
Because fixed pitch propeller turbines only have a narrow operating range where high efficiency can be achieved, it is important that they are accurately sized to suit the flow and head. Where varying flow conditions occur, it is usual to install several small units rather than one large one. This means each unit can always be run near to its optimum flow condition by shutting them down one by one to cater for reduced flows. A good design strategy is to install two units, one with twice the flow capacity of the other; then both are used under the maximum flow condition, the larger can take 2/3 of the maximum flow on its own, and the smaller can take 1/3 of maximum flow on its own. This allows efficient operation at 1/3, 2/3 and full-flow.
Turbine pumps are typically installed on a concrete platform built into a weir, as in Fig. 146. Therefore, although the turbine-pump unit is inexpensive, depending on the site, civil workings are likely to represent the largest cost-element. Pipes also will be expensive, but then for a given flow they will be equally expensive regardless of the choice of pumping system.
Higher heads or higher flows are commonly catered for by connecting turbine pumps in series or parallel.
Fig. 143 Single stage high lift turbine pump (cross-section)
Fig. 144 Multi-stage high lift turbine pump (cross-section)
Fig. 145 Turbine pump fitted with extension drive shaft (show part-sectioned)
Table 22 TYPICAL SIZES AND PRICES OF CHINESE TURBINE-PUMPS
|
Type |
Head |
Lift |
Flow |
Discharge |
Weight
(net) |
Price
(net) |
|
20-6 |
1-4 |
6-24 |
88-180 |
6-12 |
59 |
89.00 |
|
30-6 |
1-4 |
6-24 |
210-420 |
21-42 |
155 |
127.00 |
|
40-6 |
1-4 |
6-24 |
370-740 |
37-72 |
290 |
198.00 |
|
60-6 |
1-4 |
6-24 |
684-1354 |
70-142 |
985 |
571.00 |
|
60-16 |
1-6 |
16-96 |
650-1620 |
25-57 |
1374 |
1237.00 |
Table 23 COMPARISON OF IRRIGATION COSTS IN CHINA
| Type of system |
Lift |
Irrigation cost |
| Electric | 30 | 35-90 |
| Engine | 30 | 70-130 |
| Turbine pumps | 70 | 5-15 |
Table 24 SOME PERFORMANCE DATA OF SMALL TURBINE PUMPS
| Turbine pump model |
Working head (m) |
Working flow (1/a) |
Delivery head (m) |
Delivery flow (1/a) |
Shaft power (watts) | Overall efficiency (%) | |
| High yield |
10-0 |
0.5 |
15 |
3 |
0.8 |
47 |
32.8 |
| High yield |
20-4 20-6 |
0.5 1.0 |
60 84 |
2 |
7.8 6.0 |
203 570 |
42.8 |
| High yield |
30-6 |
1.0 |
190 |
6 |
16.0 |
1,340 |
50.6 |
|
Low head ZD 680 |
10-6 10-6 |
1.0 4.0 |
20 40 |
6 |
1.2 2.4 |
130 1,000 |
36.0 |
|
Low head ZD 680 |
20-6 20-6 |
1.0 6.0 |
81 198 |
6 |
6.4 15.5 |
560 8,180 |
47.0 |
|
Low head ZD 680 |
30-10 30-16 |
6.0 6.0 |
446 446 |
60 |
19.2 11.2 |
19,250 19,250 |
43.0 |
|
Medium head ZD 540 |
Z20-6 Z20-6 |
5 14 |
139 232 |
30 |
10 16 |
4,620 21,600 |
42.0 |
|
High head ZD 440 |
G20-6 G20-6 |
12 20 |
172 222 |
72 |
11 14 |
14,400 30,900 |
38.0 |
| High lift |
40-6 40-6 |
0.5 5.0 |
238 750 |
3 |
20.9 66.1 |
||
| High lift | 40-17 40-17 |
1.0 6.0 |
333 815 |
17 |
3.3 8.5 |
Fig. 146 Typical turbine pump installation
Fig. 147 Schematic diagram of hydram installation
4.9.3 The Hydraulic Ram Pump (or Hydrant)
The hydraulic ram pump, or hydram, concept was first developed by the Montgolfier brothers, better remembered for their pioneering work with hot-air balloons, in France in 1796. Essentially, a hydram (shown schematically in Fig. 147), is an automatic pumping device which utilizes a small fall of water to lift a fraction of the supply flow to a much greater height. In other words, as with the turbine pump, it uses a larger flow of water falling through a small head to lift a small flow of water through a higher head. The main virtue of the hydram is that it has no substantial moving parts, and is therefore mechanically extremely simple, which results in very high reliability, minimal maintenance requirements and a long operational life.
Its mode of operation depends on the use of the phenomenon called water hammer and the overall efficiency can be quite good under favourable circumstances. Fig. 147 illustrates the principle; initially the waste valve (1) will be open under gravity, and water will therefore flow down the drivepipe (2) from the water source (3) (having been drawn through a strainer (4) to prevent debris entering the hydram). As the flow accelerates, the hydraulic pressure under the waste valve and the static pressure in the body of the hydram (5) will increase until the resulting forces overcome the weight of the waste valve and it starts to close. As soon as it starts to close, and the aperture decreases, the water pressure in the valve body builds up rapidly and slams the waste valve shut. The moving column of water in the drivepipe is no longer able to exit via the waste valve so its velocity must suddenly decrease; this continues to cause a considerable rise of pressure which forces open the delivery valve (6) to the air-chamber (7). Once the pressure in the air chamber exceeds the static delivery head, water discharges through the delivery pipe (8). Air trapped in the air chamber is simultaneously compressed to a pressure exceeding the delivery pressure. Eventually the column of water in the .drivepipe comes to a halt and the static pressure in the casing then falls to near the static pressure due to the supply head. The delivery valve will then close, due to the pressure in the air chamber exceeding the pressure in the casing. Water will continue to be discharged through the check valve (9), after the delivery valve has closed, until the compressed air in the air chamber has expanded to a pressure equal to the delivery head. At the same time, as soon as the delivery valve closes, the reduced pressure in the casing of the hydram allows the waste valve to drop open, thereby allowing the cycle to start again.
The air chamber is a vital component, as apart from improving the efficiency of the process by allowing delivery to continue after the delivery valve has closed, it is also essential to cushion the shocks that would otherwise occur due to the incompressible nature of water. If the air chamber fills with water completely, not only does performance suffer, but the hydram body, the drivepipe or the air chamber itself can be fractured by the resulting water hammer. Since water can dissolve air, especially under pressure, there is a tendency for the air in the chamber to be depeleted by being carried away with the delivery flow. Different hydram designs overcome this problem in different ways. The simplest solution requires the user to occasionally stop the hydram and drain the air chamber by opening two taps, one to admit air and the other to release water. Another method on more sophisticated hydrams is to include a so-called snifting valve which automatically allows air to be drawn into the base of the air chamber when the water pressure momentarily drops below atmospheric pressure at the moment after flow commences when the waste valve reopens. It is important with such units to make an occasional check to see that the snifting valve has not become clogged with dirt and is working properly.
This cycling of the hydram is timed by the characteristic of the waste valve. Normally it can be either weighted or pre-tensioned by an adjustable spring, and an adjustable screwed stop is generally provided which will allow the maximum opening to be varied. The efficiency, which dictates how much water will be delivered from a given drive flow, is critically influenced by the valve setting. This is because if the waste valve stays open too long, a smaller proportion of the throughput water is pumped, so the efficiency is reduced, but if it closes too readily, then the pressure will not build up for long enough in the hydram body, so again less water will be delivered. There is often an adjustable bolt which limits the opening of the valve to a predetermined amount which allows the device to be tuned to optimize its performance. A skilled installer should be able to adjust the waste valve on site to obtain optimum performance for that particular hydram and site.
Therefore, it can be seen that the output of a hydram is constant, 24 hrs/day, and cannot readily be varied. A storage tank is usually included at the top of the delivery pipe to allow water to be drawn in variable amounts as needed.
i. Installation requirements
In a typical hydram installation, a supply head is created either by digging a small contoured diversion canal bypassing a river, or in some cases, particularly with small streams, it is normal simply to create a weir and to install the hydram directly below it.
Where greater capacity is needed, it is common practice to install several hydrams in parallel. This allows a choice of how many to operate at any one time so it can cater for variable supply flows or variable demand.
The size and length of the drivepipe must be in proportion to the working head from which the ram operates. Also, the drivepipe carries severe internal shock loads due to water hammer, and therefore normally should be constructed from good quality steel water pipe. Normally the length of the drivepipe should be around three to seven times the supply head. Also, ideally the drivepipe should have a length of at least 100 times its own diameter (eg. the design length for a 100mm (4in) drivepipe is about 10m, and for a 150mm (6in) drivepipe it is about 15m). The drivepipe must generally be straight; any bends will not only cause losses of efficiency, but will result in strong fluctuating sideways forces on the pipe which can cause it to break loose.
The hydram body needs to be firmly bolted to a concrete foundation, as the beats of its action apply a significant shock load. It should also be located so that the waste valve is always above flood water level, as the device will cease to function if the waste valve becomes submerged. The delivery pipe can be made from any material capable of carrying the pressure of water leading to the delivery tank. In all except very high head applications, plastic pipe can be considered; with high heads, the lower end of the delivery line might be better as steel pipe. The diameter of the delivery line needs to allow for avoiding excessive pipe friction in relation to the flow rates envisaged and the distance the water is to be conveyed. It is recommended that a hand-valve or check-valve (non-return valve) should be fitted in the delivery line near the outlet from the hydram, so that the delivery line does not have to be drained if the hydram is stopped for adjustment or any other reason. This will also minimize any back-flow past the delivery valve in the air-chamber and improve the efficiency.
ii. Choice of hydram design
Traditional hydram designs, such as Fig. 148, developed a century ago in Europe, are extremely robust. They tend to be made from heavy castings and have been known to function reliably for 50 years or more. A number of such designs are still manufactured in Europe and the USA in small numbers. The hydram in Fig. 148 differs from the schematic diagram of Fig. 147 in having its waste valve on the same side as the drive pipe, but its principle of operation is identical.
Lighter designs, fabricated using a welded sheet steel construction . (Fig. 149) were developed first in Japan and are now in production in other parts of SE Asia including Taiwan and Thailand. These are cheaper, but only likely to last a decade or so as they are made from thinner material which will probably eventually corrode; nevertheless they offer good value for money and are likely to perform reliably for a respectably long time. However, hydrams are mostly intended for water supply duties, operating at higher heads and lower flow rates than are normal for irrigation. Therefore it is likely that the most useful hydrams for irrigation purposes will be the larger sizes having 100-150mm (4"-6") drivepipes. Some simple designs that can be improvized from pipe fittings have also been developed by aid agencies, (such as in Fig. 150) and some interesting versions have also been quite crudely improvized using scrap materials, such as in southern Laos using materials salvaged from bombed bridges and with old propane cylinders as air chambers. Needless to say, such devices are very low in cost; the pipes in the end cost considerably more than the hydram. They are not always as reliable as traditional designs, but nevertheless are usually quite adequately reliable and are easy to repair when they fail.
| |
Fig. 148 Traditional (Blakes) European hydram design | Fig. 149 South-East Asian type of hydram |
Fig. 150 Low-cost hydraulic ram using standard pipe fittings
Table 25 HYDRAM INPUT CAPACITY
|
Nominal diameter of drive pipe |
ins. bore |
11/4 |
11/2 |
2 |
21/2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
mm. bore |
32 |
40 |
50 |
65 |
80 |
100 |
125 |
150 |
175 |
200 |
||
|
Volume of driving water required to operate the ram |
litres per minute |
from |
7 |
12 |
27 |
45 |
68 |
136 |
180 |
364 |
545 |
770 |
|
to |
16 |
25 |
55 |
96 |
137 |
270 |
410 |
750 |
1136 |
1545 |
Table 26 HYDRAM PERFORMANCE
|
Supply Head |
Delivery head (m) | |||||||||||
|
(m) |
5 |
7.5 |
10 |
15 |
20 |
30 |
40 |
50 |
60 |
80 |
100 |
125 |
|
1.0 |
144 |
77 |
65 |
33 |
59 |
20 |
12 |
|||||
|
1.5 |
|
135 |
96 |
70 |
54 |
36 |
19 |
15 |
||||
|
2.0 |
|
220 |
156 |
105 |
79 |
53 |
33 |
25 |
20 |
12 |
||
|
2.5 |
|
280 |
200 |
125 |
100 |
66 |
40 |
32 |
24 |
16 |
12 |
|
|
3.0 |
260 |
180 |
130 |
87 |
65 |
51 |
40 |
27 |
18 |
12 | ||
|
3.5 |
215 |
150 |
100 |
75 |
60 |
46 |
32 |
20 |
14 | |||
|
4.0 |
255 |
173 |
115 |
86 |
69 |
53 |
36 |
23 |
16 | |||
|
5.0 |
310 |
236 |
155 |
118 |
94 |
72 |
50 |
36 |
23 | |||
|
6.0 |
282 |
185 |
140 |
112 |
94 |
64 |
48 |
34 | ||||
|
7.0 |
216 |
163 |
130 |
109 |
82 |
60 |
48 | |||||
|
8.0 |
187 |
149 |
125 |
94 |
69 |
55 | ||||||
|
9.0 |
212 |
168 |
140 |
105 |
84 |
62 | ||||||
|
10.0 |
Litres pumped in 24 hours per 1/min of drive water. |
245 |
187 |
156 |
117 |
93 |
69 | |||||
|
12.0 |
|
295 |
225 |
187 |
140 |
113 |
83 | |||||
|
14.0 |
265 |
218 |
167 |
132 |
97 | |||||||
|
16.0 |
250 |
187 |
150 | 110 | ||||||||
|
18.0 |
280 |
210 |
169 |
124 | ||||||||
|
20.0 |
237 |
188 |
140 | |||||||||
iii. Performance characteristics
Table 25 (from [64]) indicates the input capacity of different sizes of hydram; it is this input which determines the delivery flow at a given delivery head. The lower limit indicates the minimum input flow required for practical operation, while the upper limit represents the maximum possible flow a hydram can handle. Table 26 [64] then indicates the probable litres pumped in 24 hrs for each litre/min of drive water.
Although the costs of hydrams are apparently low, as soon as high flow rates are needed at lower heads, the size of hydram and more particularly of drive pipe, begins to result in significantly higher costs. Therefore hydrams are best suited to relatively low flow rates and high head applications, (perhaps terraced tree nurseries in mountainous regions) while a turbine-pump, as discussed in the previous section, appears more attractive for the lower heads and high flow rates that are more common for irrigation of commercial crops on low-land farms.
4.9.4 Water Wheels and Norias
The undershot waterwheel is probably both the most obvious and the oldest method of extracting energy from rivers. In many cases the device simply dips into the river and is turned by the movement of the current; see Fig. 151. In the example illustrated, from Vietnam, the entire structure is made of bamboo and bamboo tubes with one end closed are mounted around the rim of the wheel. The bamboo tubes dip into the river and re-emerge filled with water, which they to near the top, where the water pours out into a trough. Devices of this kind are quite widely used in SE Asia, including China, Japan and Thailand as well as Vietnam, and are known as "norias". Fig. 152 shows a Chinese version and illustrates the principle and method of construction quite clearly. The noria is similar in many ways to the Persian wheel and was discussed earlier in Section 3.4.1.
The biggest shortcoming of the noria is that they need to be of a diameter somewhat greater than the head; this makes them fine for low head applications, but they get large and cumbersome for higher lifts. The example illustrated in Fig. 151 is 10m in diameter and is claimed to be able to irrigate about 8ha [65]. There is a small weir just visible in the illustration which creates a head of about 100mm at the base of the wheel which significantly improves the performance. The 10m diameter Vietnamese noria turns at the rate of about 1 revolution in 40 seconds and delivers water, typically, at the rate of 7 litre/sec. The cost of these Vietnamese norias is quoted as being the equivalent of US $225-450, [65]. Although the noria is attractive in being relatively inexpensive and also being capable of manufacture in the village, the sites where they may be used are limited and they are particularly prone to damage by floods. Therefore annual repair costs quoted for Vietnamese norias [65] can be as much as 30-50% of the capital cost of the installation. However, under Vietnamese conditions the same source indicated that some sample installations which were surveyed produced a return for the users in terms of value of grain production in the range 24-60% over the estimated costs.
Fig. 151 Bamboo water wheels, Vietnam
Fig. 152 Chinese type of small-scale Noria
Fig. 153 Water wheel driven coil pump (see also Fig. 50)
A modern version of the Asian noria is the floating coil pump, versions of which have been tested by the Sydfynsgruppen (supported by DANIDA) at Wema on the Tana River in Kenya, by the Danish Boy Scouts on the White Nile at Juba in southern Sudan and by the German agency BORDA on the River Niger near Bamako in Mali [66] (see Fig. 153). The principle of the coil pump is explained in Section 3.6.4 and also illustrated in Fig. 50. These recent experimental river current powered irrigation pumping systems consist of floating undershot water wheels (mounted on floating pontoons made from empty oil barrels), and by using a coil pump it is possible to use quite a small diameter water wheel and to use it to lift water to a height considerably greater than its diameter (around 10-15m is possible from a 2-3m diameter rotor).
The claimed performance of the prototype floating coil pumps was 6.6 litre/sec against a delivery head of 5m with a river current velocity of 1.2 m/s on the Tana River at Wema. For reasons which are not known, the similar unit tested on the Nile only pumped 0.7 litre/sec against 5m head with the same river current velocity of 1.2m/s. Quite high current velocities in the range from l-2m/s (2-4 knots) are necessary for devices of this kind. The Kenyan machine was made mainly from glass-reinforced plastic (fibreglass) and cost US $4 000 in 1979, but the much less efficient Sudan prototype used steel and wood, with flexible plastic pipe for the coil pump and only cost $350 In both cases the considerable length of flexible pipe required accounted for about one third of the total cost.
The Royal Irrigation Department of Thailand has developed a similar floating undershot waterwheel device to those just described, but in this case the wheel is mechanically linked to a conventional piston pump by means of sprockets and chains. It requires a minimum current velocity of lm/s with a river flow of at least 0.6m3/s and it is claimed to be capable of pumping from 0.3-1.5 litre/sec to heads of 60m-15m respectively. The cost was quoted at $1 450, not including the delivery piping and header tank.
A general problem with water wheels is that if the drive is taken from the main shaft, the costs become high in relation to the power available, because large slow-moving (and therefore expensive) mechanical drive components are needed to transmit the high torque involved. Also, with shafts only turning at between 1-5 rpm (which is typical of waterwheels) either very large pump swept volumes are required or a lot of gearing up is necessary to drive a smaller pump at an adequate speed; either way the engineering is expensive in relation to the power. Therefore waterwheels, although apparently offering simple solutions, are not always as easy to adapt for powering mechanical devices such as pumps as might at first be expected.
4.9.5 Novel Water-Powered Devices
i. The Plata Pump
An unconventional alternative to a small water wheel for powering a small pump is the Plata Pump (Fig. 154) . This device was invented in New Zealand and some efforts have been made to commercialize it internationally, although it is not believed to be very widely used. In it, a series of small turbine rotors are mounted on a single shaft along the axis of a cylindrical duct, approximately 2.5m long by 0.5m in diameter. It is a bit like a multi-rotored propeller turbine, although there are no diffusers or other static blades to control rotation of the fluid. The shaft drives two opposed single-acting piston pumps via a crank. The Plata Pump is intended to be mounted in a low dam or weir, so that it slopes at a slight angle and water runs downhill through it. It is not supposed to run full of water, but works best when running around 1 to J full; perhaps because when running full the flow rotates and thereby causes loss of efficiency.
Fig. 154 Cut-away view showing general arrangement of a Plata pump installation
The Plata Pump is designed to operate on heads of 0.25-lm; usually this is engineered by placing the Plata Pump at an appropriate angle on a stream bed and building up a weir with rocks or other material to create the necessary head. The overall efficiency of the Plata Pump has been measured as being in the 6-30% range at delivery heads from 6-90m; [66], The best efficiency was recorded at 24m head. Typical performance with a working flow of 85 litre/sec is 1.3 litre/sec at 6m, 0.25 litre/sec at 24m, 0.11 litre/sec at 38m. A working flow of 153 litre/sec was necessary to allow 90m delivery head to be reached.
The price of the Plata Pump in kit form was about US $2 000 in 1980, [66], so it seems to be relatively expensive in relation to its performance in comparison, for example, with Chinese turbine pumps described earlier. It also appears to be less efficient and robust than the turbine pump.
ii. The river current turbine
The energy of motion (or kinetic energy) available in river or canal currents is, exactly as for wind, proportional to the cube of the velocity. The relationship between power and velocity is:
where p is the density of water (1000kg/m3 for fresh water), A is the area of cross section of current in m2 and V is the mean velocity through the cross-section in m/s. From this the following power densities can be calculated, as shown in Table 27:
Table 27 POWER DENSITY IN WATER CURRENTS AS A FUNCTION OF WATER VELOCITY
|
velocity |
(m/s) |
0.5 |
1.0 |
1.5 | 2.0 |
| (knots) |
1.0 |
2.0 |
3.0 | 4.0 | |
|
power density |
(kW/m2) |
0.06 |
0.5 |
1.7 | 4.0 |
It is interesting to compare this with Table 16 giving the equivalent result for wind; similar power is experienced in water at about 1/9 the velocity in wind needed to achieve the same power, due to the much higher density of water. Since a mean wind speed of 9m/s would be considered most attractive for the economic use of wind power, it is clear that even currents of lm/s may be more than adequate as a power source if they could be exploited efficiently. Moreover, a major problem with exploiting wind energy is its great variability, but river currents generally flow steadily 24 hours per day, [67].
The traditional and most obvious technique, undershot water wheels, are an inefficient means to exploit currents, since the bulk of the machine is external to the water at any one time and therefore provides no power. Therefore the Intermediate Technology Development Group (UK) undertook a programme, financed by the Netherlands Government, to develop turbines which would operate efficiently entirely submerged to extract shaft power from river currents; (the author must declare an interest, since the device in question was developed under his technical supervision).
The main device tested is a vertical axis cross-flow turbine similar to the Darrieus windmill in principle (see Section 4.7.2). It has the advantage that the vertical drive shaft conveniently comes through the surface, so that any mechanical components can be located on the deck of a pontoon above water. Unlike a water wheel this device can intercept a comparatively large cross-section of current using little material other than a rotor to do so; moreover it turns relatively fast in relation to the current (13.5rpm in this case with a lm/s current) which reduces the gearing needed to drive a pump at a reasonable speed. The concept is illustrated in Fig. 155 , while an actual working irrigation pumping unit, installed on the white Nile near Juba in southern Sudan, worked reasonably reliably, was fitted with a 3m diameter vertical axis rotor (3.75m2 cross-sectional area) powering a centrifugal pump via a two stage toothed belt speed increaser. It was tested and found to pump approximately 3.5 litre/sec through a head of 5m with a current of 1.2m/s. The rotor efficiency is 25 to 30% (as with a small windmill) and an overall system efficiency of 6% has been achieved, including pipe losses as well as pump and transmission losses. The prototype, which cost the equivalent of US $5 000 to build, has been used successfully to irrigate a 6ha vegetable garden. Smaller, simpler, low-cost versions were also tested near Juba. Costs are difficult to determine with prototypes, but the device appears to be potentially economically attractive.
Fig. 155 IT river current turbine pump
The potential for using the river to pump its own water has been demonstrated, but further work will be needed to optimize this device and adapt it for commercial production. However, the considerable power potential in many river, canal and for that matter tidal currents should ensure that this at present little known and little thought of power source gains increasing recognition, and will eventually be made use of. This is particularly because many large rivers (such as the Nile, Euphrates, Zambesi, Indus), flow through regions which are arid or which have several months of dry season.
Opening (from Psalm 104)
1 You appointed the moon to mark the seasons,*
and the sun knows the time of its setting.
2 You make darkness that it may be night,*
in which all the beasts of the forest prowl.
3 May the glory of the Lord endure for ever;*
may the Lord rejoice in all his works.
4 May these words of mine please him;*
I will rejoice in the Lord.Psalm 1
nor lingered in the way of sinners, nor sat in the seats of the scornful!
2 Their delight is in the law of the Lord,*
and they meditate on his law day and night.
3 They are like trees planted by streams of water, bearing fruit in due season, with leaves that do not wither;*
everything they do shall prosper.
4 It is not so with the wicked;*
they are like the chaff which the wind blows away.
5 Therefore the wicked shall not stand upright when judgment comes,*
nor the sinner in the council of the righteous.
6 For the Lord knows the way of the righteous,*
but the way of the wicked is doomed.
you set me free when I am hard-pressed;
have mercy on me and hear my prayer.
2 ‘You mortals, how long will you dishonour my glory;*
how long will you worship dumb idols and run after false gods?’
3 Know that the Lord does wonders for the faithful;*
when I call upon the Lord, he will hear me.
4 Tremble, then, and do not sin;*
speak to your heart in silence upon your bed.
5 Offer the appointed sacrifices*
and put your trust in the Lord.
6 Many are saying
‘Oh, that we might see better times!’*
Lift up the light of your countenance upon us, O Lord.
7 You have put gladness in my heart,*
more than when grain and wine and oil increase.
8 I lie down in peace; at once I fall asleep;*
for only you, Lord, make me dwell in safety.
How to Make a Hydraulic Ram Pump
Contents
Short Description
- Definition: A hydraulic ram is a water-powered cyclic pump
- Idea: Pump Water to a higher point than where the water originally started
- Information Type: Principles
- Price Range: £1500 for small 2-inch drive pipe sizes up to £5000 for 4-inch or 6-inch sizes
Introduction
The hydraulic ram pump, or hydram, concept was first developed by the Mongolfier brothers in France in 1796 (they are better remembered for their pioneering work with hot-air balloons).
Essentially, a hydram is an automatic pumping device which utilises a small fall of water to lift a fraction of the supply flow to a much greater height; ie it uses a larger flow of water falling through a small head to lift a small flow of water through a higher head. The main virtue of the hydram is that its only moving parts are two valves, and it is therefore mechanically very simple. This gives it very high reliability, minimal maintenance requirements and a long operation life.
How a hydram works
Its mode of operation depends on the use of the phenomenon called water hammer and the overall efficiency can be quite good under favourable circumstances. More than 50% of the energy of the driving flow can be transferred to the delivery flow.
Figure 1 illustrates the principle; initially the impulse valve (or waste valve since it is the non-pumped water exit) will be open under gravity (or in some designs it is held open by a light spring) and water will therefore flow down the drive pipe (through a strainer) from the water source. As the flow accelerates, the hydraulic pressure under the impulse valve and the static pressure in the body of the hydram will increase until the resulting forces overcome the weight of the impulse valve and start to close it. As soon as the valve aperture decreases, the water pressure in the hydram body builds up rapidly and slams the impulse valve shut. The moving column of water in the drive pipe is no longer able to exit via the impulse valve so its velocity must suddenly decrease; this continues to cause a considerable rise of pressure which forces open the delivery valve to the air-chamber.
Once the pressure exceeds the static delivery head, water will be forced up the delivery pipe. Air trapped in the air chamber is simultaneously compressed to a pressure exceeding the delivery pressure. Eventually the column of water in the drive pipe comes to a halt and the static pressure in the casing then falls to near the supply head pressure. The delivery valve will then close, when the pressure in the air chamber exceeds that in the casing. Water will continue to be delivered after the delivery valve has closed until the compressed air in the air
Figure 1: The hydraulic ram pump
The air chamber is a vital component, as apart from improving the efficiency of the process by allowing delivery to continue after the delivery valve has closed, it is also essential to cushion the shocks that would otherwise occur due to the incompressible nature of water. If the air chamber fills with water completely, not only does performance suffer, but the hydram body, the drive pipe or the air chamber itself can be fractured by the resulting water hammer. Since water can dissolve air, especially under pressure, there is a tendency for the air in the chamber to be depleted by being carried away with the delivery flow. Different hydram designs overcome this problem in different ways. The simplest solution requires the user to stop the hydram occasionally and drain the air chamber by opening two taps, one to admit air and the other to release water. Another method on more sophisticated hydrams is to include a so-called snifting valve which automatically allows air to be drawn into the base of the air chamber when the water pressure momentarily drops below atmospheric pressure. It is important with such units to make an occasional check to see that the snifting valve has not become clogged with dirt and is working properly.
Figure 2: The hydraulic ram pump system
This cycling of the hydram is timed by the characteristic of the waste valve. Normally it can be weighted or pre-tensioned by an adjustable spring, and an adjustable screwed stop is generally provided which will allow the maximum opening to be varied. The efficiency, which dictates how much water will be delivered from a given drive flow, is critically influenced by the valve setting.
This is because if the waste valve stays open too long, a smaller proportion of the throughput water is pumped, so the efficiency is reduced, but if it closes too readily, then the pressure will not build up for long enough in the hydram body, so again less water will be delivered. There is often an adjustable bolt which limits the opening of the valve to a predetermined amount which allows the device to be turned to optimise its performance. A skilled installer should be able to adjust the waste valve on site to obtain optimum performance. Therefore, it can be seen that the output of a hydram will be constant and is non-adjustable. A storage tank is usually included at the top of the delivery pipe to allow water to be drawn in variable amounts as needed.
Installation requirements
Figure 2 illustrates a typical hydram installation, pumping water to a small storage tank on a plateau. It can be seen that the supply head is created in this case by creating a weir. In some cases a small stream is diverted to provide the water supply.
Where greater capacity is needed, it is common practice to install several hydrams in parallel. This allows a choice of how many to operate at any one time so it can cater for variable supply flows or variable demand. The size and length of the drive pipe must be in proportion to the working head from which the ram operates. Also, the drive pipe carries severe internal shock loads due to water hammer, and therefore normally should be constructed from good quality steel water pipe. Normally the length of the drive pipe should be around three to seven times the supply head. Ideally the drive pipe should have a length of at least 100 times its own diameter. The drive pipe must generally be straight; any bends will not only cause losses of efficiency, but will result in strong fluctuating sideways forces on the pipe which can cause it to break loose.
The hydram body requires to be firmly bolted to a concrete foundation, as the beats of its action apply a significant shock load. The hydram should be located so that the waste valve is always located above flood water level, as the device will cease to function if the waste valve becomes submerged. The delivery pipe can be made from any material capable of carrying the pressure of water leading to the delivery tank. In all except very high head applications, plastic pipe can be considered; with high heads, the lower end of the delivery line might be better as steel pipe. The diameter of the delivery line needs to allow for avoiding excessive pipe friction in relation to the flow rates envisaged and the distance the water is to be conveyed. It is recommended that a hand-valve or check-valve (non-return valve) should be fitted in the delivery line near the outlet from the hydram, so that the delivery line does not have to be drained if the hydram is stopped for adjustment or any other reason. This will also minimise any back flow past the delivery valve in the air chamber and improve efficiency.
Choice of hydram design
Traditional hydram designs, such as in Figure 3, developed a century ago in Europe, are extremely robust. They tend to be made from heavy castings and have been known to function reliably for 50 years or more. However, although a number of such designs are still manufactured in Europe and the USA in small numbers, they are relatively expensive, although generally speaking the drive-pipe, delivery pipe and civil workings will be significantly more expensive than even the heaviest types of hydram.
Lighter designs, fabricated using a welded sheet steel construction, were developed first in Japan and are now in production in other parts of SE Asia including Taiwan and Thailand. These are cheaper, but only likely to last a decade or so as they are made from thinner material which will eventually corrode. Nevertheless they offer good value for money and are likely to perform reliably.
Figure 3: Traditional hydram design
Hydrams are mostly intended for water supply duties, in hilly or mountainous areas, requiring small flow rates delivered to high heads. They are less commonly used for irrigation purposes, where the higher flow rates required will usually demand the use of larger sizes of hydram having 6-inch or 4-inch drive pipes. Manufacturers usually describe the size of a hydram by the supply and delivery pipe diameters (generally given in inches even in metric countries because of the common use of inch sizes for pipe diameters); eg a 6 x 3 hydram has a 6-inch diameter drive pipe and a 3-inch diameter delivery pipe.
Some simple designs that can be improvised from pipe fittings have also been developed by aid agencies (Figure 4), and some interesting versions have also been quite crudely improvised using scrap materials, such as a unit which is being produced in some numbers in southern Laos from materials salvaged from bombed bridges and using old propane cylinders for the air chamber. Needless to say, such devices are very low in cost but the pipes in the end cost considerably more than the hydram. They are not always as reliable as traditional designs, but are usually acceptably reliable with failures separated by many months rather than days, and are easy to repair when they fail.
Figure 4: A ram pump made from standard pipe fittings
Performance characteristics
Table 1 indicates estimated performance for typical 4-inch x 2-inch and 6-inch x 3-inch commercial hydrams.
|
Hydram size in inches |
4" X 2" |
| ||||||
|
Head Ratio |
5 |
1015 |
20 |
5 |
10 |
15 |
20 | |
|
Driven flow (litres/sec) |
8.96 |
9.7 |
10 |
9.02 |
20.2 |
17.2 |
17.1 |
19.3 |
|
Delivery (m3/day) |
94 |
51 |
35 |
23 |
216 |
101 |
69 |
50 |
Table 1: Estimated performance of hydrams
Costs
The costs of commercial hydrams are typically in the range from about £1500 for small 2-inch drive pipe sizes up to as much as £5000 for 4-inch or 6-inch sizes. The cost of the drive pipe can also be quite high for the larger sizes. Therefore hydrams are best suited to relatively low flow rates and high head applications.
Of course there are no fuel costs and negligible maintenance costs associated with hydrams.
Further information
References
• Jeffery, T D, Thomas T H, Smith A V, Glover, P B, Fountain P D Hydraulic Ram Pumps: A guide to ram pump water supply systems - IT Publications, 1992
• Iversen H W 'An Analysis of the Hydraulic Ram' - Journal of Fluids Engineering, Transactions of the American Society of Mechanical Engineers - June 1975.
• Kindel E W 'A Hydraulic Ram for Village Use' - Volunteers in Technical Assistance, Arlington, VA, USA - 1970 and 1975.
• Hofkes and Visscher Renewable Energy Sources for Rural Water Supply in Developing Countries - International Reference Centre for Community Water Supply and Sanitation, The Hague, The Netherlands - 1986.
• Watt S B A Manual on the Hydraulic Ram for Pumping Water - ITDG Publishing, 1975.
Suppliers
Note: This is a selective list of supplies and does not imply endorsement by Practical Action.
|
Green and Carter Rams |
John Blake Ltd. |
|
Vulcan Works |
P.O.Box 43 |
|
Ashbrittle |
Royal Works |
|
Wellington |
Atlas Street |
|
Somerset |
Clayton Le Moors |
|
TA21 0LQ. |
Lancashire, BB5 5LP |
|
United Kingdom |
United Kingdom |
|
Tel: +44 (0)1823 672365 |
Tel: 01254 235441 |
|
Fax: 01254 382899 | |
|
| |
|
Website: http://www.allspeeds.co.uk |
Useful Addresses
Development Technology Unit (DTU)
School of Engineering
University of Warwick
Coventry CV4 7AL
United Kingdom
Tel: +44 (0)1203 522339
Fax: +44 (0)1203 418922
Website: http://www.eng.warwick.ac.uk/DTU
http://www.eng.warwick.ac.uk/DTU/pubs/lift.html
Development Technology Unit who has carried out a lot of research into simplifying the construction of hydraulic ram pumps. The DTU is a research unit within the School of Engineering at the University of Warwick in the UK. The aim of the DTU is to research and promote appropriate technologies for application in Developing Countries.
WOT - Werkgroep Ontwikkelingstechnieken
Working Group on Development Techniques
Vrijhof 205/206
P.O.Box 217
7500 AE Enschede
Netherlands
Tel: +31 53 489 3845
Fax: +31 53 489 2671
Website: http://www.wot.utwente.nl
WOT is a non-profit organisation working in the field of small-scale sustainable energy, based at the University of Twente, Netherlands.
References and further reading
This Howtopedia entry was derived from the Practical Action Technical Brief Water.
To look at the original document follow this link: http://www.practicalaction.org/?id=technical_briefs_water
http://en.wikipedia.org/wiki/Hydraulic_ram
Useful addresses
Practical Action
The Schumacher Centre for Technology & Development, Bourton on Dunsmore, RUGBY, CV23 9QZ, United Kingdom.
Tel.: +44 (0) 1926 634400, Fax: +44 (0) 1926 634401
e-mail: practicalaction@practicalaction.org.uk
web: www.practicalaction.org
Related Articles
- How to Build Human-Powered Water-Lifters
- How to Build an Underground Brick Dome Water Tank
- How to Make a Hand Pump
- How to Make a Solar Pump
- How to Make a Hydraulic Ram Pump
- How to Build a Windpump (Principles)
- How to Use Diesel Engines
- How to Use Photovoltaic Energy
- How to Use Sun Power
- How to Use the Porous Clay Pots and Pipes System
- Micro Irrigation
Two ways to support the work of howtopedia for more practical articles on simple technologies:
Support us financially or,
Testimonials on how you use howtopedia are just as precious: So write us !
<paypal />
Categories
- This page was last edited on 23 April 2010, at 18:50.
- Content is available under GNU Free Documentation License 1.2 unless otherwise noted.
- Privacy policy
- About Howtopedia - english
- Disclaimers
Posts
